BOD quality control
Limit of detection (LOD)
BOD detection limits are theoretically based. A key assumption which the concept of detection for BOD is based is that the LEAST amount of depletion allowable is 2 mg/L. The LOD is also based on the highest volume of sample used in a dilution series. What results is the detection capability for a specific dilution series, or sample. This technique doesn’t should include seed correction, because we want to identify depletion due to the sample itself, and not due to the seed material.
The calculation involved is simply:
| If the highest sample volume used is: | The LOD for that sample is: |
|---|---|
| 300 mL | 2 mg/L |
| 200 mL | 3 mg/L |
| 100 mL | 6 mg/L |
| 75 mL | 8 mg/L |
| 50 mL | 12 mg/L |
Blanks
Oxygen depletion MUST be < 0.25 mg/L.
Seed controls
- Need at least one passing dilution
- Best to do 3 dilutions
- Calculate seed correction factor
- Standard Methods has changed its position on this. Less emphasis on seed control; More on GGA performance
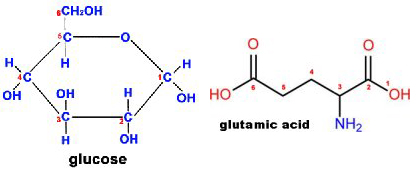
Glucose-glutamic acid (GGA)
- Must be glucose + glutamic acid ("Alphatrol" not allowed)
- GGA solution MUST be 150 mg/L of each
- Must bring up to room temperature before use.
- Never pipet out of the GGA reagent bottle
- Must use exactly 6 mLs of GGA solution
- Must be seeded
- Acceptance criteria MUST be 198 + 30.5 (167.5-228.5 mg/L)
- If you prepare more than one, ALL must meet criteria
- Consider the case where GGA #1 = 150, GGA #2 = 250, average=200
- Would this constitute acceptable performance???????
- What about two results: 225 and 230 mg/L
- ...or results of 165 and 175?
- Analysis required weekly (1 per 20 if > 20 samples/week)
- Glucose
- C6H12O6
- Molecular Weight= 180.16
- Glutamic acid
- C5H9NO4
- Molecular Weight= 147.13
- Atomic Mass of nitrogen (N) is 14
thus nitrogen represents 14/147.13 or 9.5% of the mass of glutamic acid - GGA is a 50:50 mix of glucose and glutamic acid
thus Nitrogen represents about 4.75% of the weight of GGA - Critical point: There’s nitrogen in GGA!!!
That means that if your seed source contains nitrifiers, then your GGA will be biased high as the nitrifiers use oxygen to convert the nitrogen ammonia and then to nitrate
That further means that if your facility recycles final effluent into primary clarifiers-- and you use primary as your seed source --you could be adding nitrifying organisms to the seed. The result could mean high bias in your GGA data.
Precision (Replicates)
Precision is a measure of how closely multiple determinations performed on the same sample will agree with each other. To examine precision under the brightest light, consider the implications of analyzing replicates of a final effluent sample in which one of the determinations measures only 80% of a daily maximum permit limit, and the other exceeds the daily maximum by 20%.
Which result is correct? One would have an overwhelming desire to report the value that is under the daily maximum, but is that a correct, or even defensible approach? The simple answer is, "No."
The difference between the results of replicate analyses, the duplicate range, is used to assess the precision (reproducibility) of the test method. Statistical treatment of replicates is as follows:
Replicate essentials
- Must use same dilutions as used for sample
- Example: if effluent dilutions are 100, 200, and 300 mL, then replicate must be 100, 200, and 300 mL
- Recommended after every 20 samples of the same matrix
- Influent and effluent are considered separate matrices
- If you analyze industrial samples, those are a separate matrix as well
Evaluating replicates
Precision, in BOD, is based on absolute difference (Range) or relative percent difference (RPD) between duplicates.
Absolute Difference
The term "absolute difference" is a mathematical expression that means the result cannot be less than zero. A negative result becomes positive. Therefore, the absolute difference of 1-3 is 2 (the negative 2 becomes a positive). One way to look at this is that the smaller of two values is always subtracted from the larger value.
- Range
- Range is expressed in the same units as values (i.e., mg/L)
Range is the absolute difference of the larger value – smaller value
Example Sample = 22 Replicate =18
Range = 22 - 18 = 4
- RPD (Relative Percent Difference)
- RPD is expressed as %
RPD = [Range of replicates) ÷ Mean (of replicates)] X 100
Example Sample = 22 Replicate =18
Range = 22- 18
Range = 4 (see above)
Mean= (22 + 18) ÷ 2 = 40 ÷ 2 = 20
RPD = (4 ÷ 20) x 100 = 20%
Range is concentration dependent
Concentration dependency means that as concentration changes, so does the range. If you were told that a lab's range control limit was 25 mg/L, and asked whether that was "good", your response would likely be that you don't have enough information to make an assessment. If you were told that it was associated with effluent samples, you may now say something along the lines of "That's terrible!". On the other hand, if you were told that the range control limit of 25 was for influents, you may reverse your earlier assessment.
That is precisely what "concentration dependency" implies: that you need to know the concentrations involved in order to evaluate the precision.
- If the two values in question are 500 and 525, a range of 25 indicates very good precision.
- But…if the two values are 30 and 5, a range of 25 now indicates extremely POOR precision.
- The use of RPD (instead of Range) offers a means of normalizing this variance.
- With values of 500 and 525, the RPD is 4.9%
- With values of 5 and 30, however, the RPD is 143%
- You still need to know that the lower the RPD, the better the precision, but knowing that, the disparity between these sets of replicates becomes clear.
How do you deal with concentration dependency?
- Establish separate control limits based on concentration range
- Example: A typical BOD effluent may range 5-10 mg/L, but following rain events often runs 20-30 mg/L. During rain events, range of replicates may exceed control limits!
- Establish interim limits to deal with non-routine concentrations.
Which to use to monitor precision? Range or RPD?
As concentration increases, the absolute range usually increases as well with no change in RPD.
For a given range, as concentration increases, RPD decreases.
For a given range, as concentration decreases, RPD increases.
When might this be of use?
If your system is susceptible to high I & I ...OR....
If your system exhibits high variability in influent loading
It might be a good idea to use RPD for raw (influent) and range for final (effluent).
Control limits
RPD Control limits
- Test the data for and eliminate outliers before proceeding.
- Calculate the mean and standard deviation of the data.
- Upper warning limit = Mean + 2 standard deviations
- Upper control limit = Mean + 3 standard deviations
NOTE: RPD is a "1-tailed test" (which means you can't have an RPD less than zero), so we use only UPPER control limits. The target for spike recovery is 100%, and recoveries can be both less than and greater than 100%. Therefore, spike control limits have upper and LOWER control limits, termed a "two-tailed" test.
Range Control Limits
Arithmetic Mean
The arithmetic mean is calculated by summing the data involved and divided by the number of data points.
- Test the data for and eliminate outliers before proceeding.
- Calculate the mean of the data.
- Warning limits = 2.51 x Mean of the data
- Control limits = 3.27 x Mean of the data
Calculating Replicate Control Limits
Precision is a measure of how closely multiple determinations performed on the same sample will agree with each other. To examine precision under the brightest light, consider the implications of analyzing replicates of a final effluent sample in which one of the determinations measures only 80% of a daily maximum permit limit, and the other exceeds the daily maximum by 20%.
Which result is correct? One would have an overwhelming desire to report the value that is under the daily maximum, but is that a correct, or even defensible approach? The simple answer is, "No."
Replicate analyses for all requested parameters are performed regularly after every 20 samples. The difference between the results of replicate analyses, the duplicate range, is used to assess the precision (reproducibility) of the test method. Statistical treatment of replicates is as follows:
R = |(Sample mg/L) - (Replicate mg/L)|
where: |expression | = the absolute value of "expression"
NOTE: The absolute value simply means that negative values are converted to positive values, thus |2 - 5| = 3 rather than -3. Range can be thought of as the difference between two sample results that is always a positive value.
Step 1 - Calculate the range (R) of each set of replicate samples
Step 2 - Calculate the average Range (of at least 20 replicate pairs)
The average range [R] is calculated for n replicate sample sets (to be statistically significant, n must be at least 20):
| Sample BOD Effluent Replicate Data | ||||||
|---|---|---|---|---|---|---|
| Sample | Replicate | Range | Sample | Replicate | Range | |
| 3.5 | 5.0 | 1.5 | 9.3 | 8.5 | 0.8 | |
| 14.3 | 13.2 | 1.0 | 17.2 | 16.1 | 1.1 | |
| 3.0 | 3.0 | 0.0 | 10.2 | 10.1 | 0.1 | |
| 11.7 | 10.7 | 1.0 | 7.5 | 8.7 | 1.2 | |
| 3.7 | 3.3 | 0.4 | 12.2 | 11.7 | 0.5 | |
| 4.1 | 3.3 | 0.8 | 5.9 | 5.0 | 0.9 | |
| 10.2 | 9.2 | 1.0 | 15.4 | 15.0 | 0.4 | |
| 6.0 | 6.1 | 0.1 | 6.2 | 7.0 | 0.8 | |
| 22.3 | 19.5 | 2.8 | 17.4 | 23.2 | 5.8 | |
| 8.0 | 7.8 | 0.2 | 3.6 | 5.7 | 2.1 | |
| Sum = 22.6 # data points (N) = 20 Mean {R} = 1.13 |
||||||
Step 3 - Calculate control limits
Control and warning limits are calculated:
Control Limit (CL)= 3.27 × {R}
for the data set above, CL = 1.13 × 3.27 = 3.69
Warning Limit (WL) = 2.51 × {R}
for the data set above, WL = 1.13 × 2.57 = 2.90
Identifying outlier data
A number of statistical tests to identify outliers are available, including a procedure used by the U.S.G.S., Dixon's test, the t-test, and Grubbs' test. While any of these tests can be employed to identify outlier data, Grubbs' test will be mentioned here due to its relative simplicity.
First, it is critical to understand that the basic premise of any outlier test is simply to assign a statistical likelihood that a given suspect outlier point represents a different population than the other values in a data set. It cannot -and should not-tell you what to do with that point. Because, however, the consequences associated with failing to exclude outliers (control limits become unreasonably broad allowing inaccurate data) far outweighs the risk of excluding them (control limits become too tight and too many data points become suspect), we recommend that outliers be excluded from further use.
Grubbs' test is based on the calculation of a "Z-score" which is then evaluated against a set of criterion values based on the number of data points in the data set.
Z-score (Z) =
| Mean - [Suspect result] |
------------------------------
standard deviation
where: | expression | = absolute value of "expression"
If the resultant Z-score is greater than the corresponding criterion value based on the number of data points, then the suspect value is indeed an outlier, and should be excluded and the control limits re-calculated.
Grubbs outlier test example
Given the following data set:
1.5, 1.1, 0.0, 1.0, 0.4, 0.8, 1.0, 0.1, 2.7, 0.2, 0.8, 1.1, 0.1, 1.2, 0.5, 0.9, 0.4, 0.8, * 5.8 *, 2.1
First, order the data from smallest to largest:
0, 0.1, 0.1, 0.2, 0.4, 0.4, 0.5, 0.8, 0.8, 0.8, 0.9, 1.0, 1.0, 1.1, 1.1, 1.2, 1.5, 2.1, 2.7, * 5.8 *
You would test only the maximum value (5.8). The mean for the data set (including the suspect point) is 1.13, and the standard deviation is 1.294. This yields a Z-score of 3.631 for the maximum range value (5.8) in the data set.
The Z-criterion value for a set of 20 data points is 2.71. Since the suspect data point's Z-score is greater than the criterion Z-score, the suspect data point (5.8) is indeed an outlier. The data point must be removed, and the outlier test repeated using the next highest point (2.7).
Using the ordered data without the "5.8" value:
0, 0.1, 0.1, 0.2, 0.4, 0.4, 0.5, 0.8, 0.8, 0.8, 0.9, 1.0, 1.0, 1.1, 1.1, 1.2, 1.5, 2.1, * 2.7 *
Now we test the new maximum value (2.7). The mean for the reduced data set (including the suspect point) is 0.879, and the standard deviation is 0.689. This yields a Z-score of 2.64.
Subtract the mean from the suspect data point (2.7 - 0.88)= 1.82.
Then divide 1.82 by the standard deviation (0.689) 1.82 ÷ 0.689= 2.64.
The Z-criterion value for a set of 19 data points is 2.68. Since the suspect data point's Z-score is LESS than the criterion Z-score (although just barely!), the suspect data point (2.7) is NOT an outlier.
Control limits can now be calculated, using the data from the 19-point data set.
The control and warning limits are calculated:
Control Limit (CL) = 3.27 × {R}
for the data set above, CL = 0.88 × 3.27 = 2.88
Warning Limit (WL) = 2.51 × {R}
for the data set above, WL = 0.88 × 2.57 = 2.26
The Range Control limits resulting from the inclusion of this data point would be 2.88 (Warning Limit = 2.26), while if the outlier data point is NOT excluded, the control limit would be 3.69 (Warning Limit = 2.90).
| # Data Points | Critical Z-score | # Data Points | Critical Z-score | # Data Points | Critical Z-score | # Data Points | Critical Z-score | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 1.15 | 15 | 2.55 | 27 | 2.86 | 39 | 3.03 | |||
| 4 | 1.48 | 16 | 2.59 | 28 | 2.88 | 40 | 3.04 | |||
| 5 | 1.71 | 17 | 2.62 | 29 | 2.89 | 50 | 3.13 | |||
| 6 | 1.89 | 18 | 2.65 | 30 | 2.91 | 60 | 3.20 | |||
| 7 | 2.02 | 19 | 2.68 | 31 | 2.92 | 70 | 3.26 | |||
| 8 | 2.13 | 20 | 2.71 | 32 | 2.94 | 80 | 3.31 | |||
| 9 | 2.21 | 21 | 2.73 | 33 | 2.95 | 90 | 3.35 | |||
| 10 | 2.29 | 22 | 2.76 | 34 | 2.97 | 100 | 3.38 | |||
| 11 | 2.34 | 23 | 2.78 | 35 | 2.98 | 110 | 3.42 | |||
| 12 | 2.41 | 24 | 2.80 | 36 | 2.99 | 120 | 3.44 | |||
| 13 | 2.46 | 25 | 2.82 | 37 | 3.00 | 130 | 3.47 | |||
| 14 | 2.51 | 26 | 2.84 | 38 | 3.01 | 140 | 3.49 |
Corrective action
To put it simply, corrective action is required whenever any control limit is exceeded. The goal of corrective action is to develop a historical record which details the type of problems a laboratory encounters as well as the resolution process itself. To put this into perspective, most operators who have analyzed BOD using a DO probe come to realize that the DO probe membrane degrades over time, and at some certain point, you need to replace it. Most of this information, unfortunately, is kept in the operator's head. A new operator-perhaps an individual without extensive analytical experience-who takes over laboratory responsibilities, may not recognize the "warning signs" that indicate a need to change the membrane.
Without a corrective action trail, which essentially can be reduced to documentation in the form of "When you see this, do the following", analysis will continue, until the fateful day that a GGA sample fails to meet acceptance criteria. Once data has been generated under circumstances in which one or more QC checks exceed their associated acceptance criteria, it is too late, and further effort is mandatory.
Corrective action, then, should be considered to be a sort of preventive medicine against future illnesses. We should learn from our past "difficulties" to guard against going through the same difficulties in the future. As an example, the first time one ever "messes" with a bee's nest, they tend to get stung. The best corrective action for this situation might simply be to stay away from bee's nests. Is that the only corrective action for this situation? Certainly not! The kid that chooses a corrective action of simply throwing the rock (at the bee's nest) from further away may find, however, that his "corrective action" was not adequate to correct the "problem".
A laboratory needs to document the results obtained from all corrective action efforts so that in the future, the operator/analyst can "home in" on the right solution for a particular problem. A good example of this is to consider what corrective action might be taken in response to failing a matrix spike control limit for recovery. In this example, let's say an operator records a matrix spike recovery of 52% for total phosphorus. Being in a hurry, as many things need to be done around the village, the operator's corrective action is to review his calculations to make sure he didn't make a simple math error. Satisfied that no error was made with calculations, he shrugs his shoulders, chalks it up to fate, and goes about his other duties.
This same process goes on for several weeks, and over that time, he gets recoveries between 42% and 58%. He's heard about matrix interferences, and figures that his effluent has suddenly developed a matrix interference. Six months later, however, it's time for an evaluation of his laboratory and the DNR auditor discovers that the real problem is that the standard used to prepare matrix spikes not only should have been prepared fresh 3 months ago, but that an error was made during the preparation. The spike solution is found to be exactly one-half of the concentration the operator believed it to be.
Remember...we need to be sure that the corrective action taken in response to a QC failure is appropriate for the problem at hand, and the laboratory needs to establish a system to check back and ensure that the problem has actually been solved. After all, if one brings their car into the garage to have it looked at because it won't start, they would not be happy to hear that the mechanic's "corrective action" included performing a costly re-alignment!
Last resort - Qualifying your results
Operators will still need to report those analytical results that are associated with any analytical run in which one or more of the quality control samples fails to meet acceptance criteria. These data must be flagged on the DMR reports by putting a check on the Quality Control line in the upper right hand corner of the form as well as by circling or marking the affected data with an asterisk. It is also acceptable to include a narrative that describes which dates and analyses are affected, and specific details regarding the reason for qualification of the data. The operator must also decide whether or not to include the analytical results when calculating weekly or monthly average values. If the decision is made to exclude the values in question from calculating weekly/monthly averages, an explanation for the exclusion(s) must also be provided.
Documentation and record-keeping
All records of equipment calibration and maintenance, QC tests, sampling, and sample analysis are retained for at least three (3) years [five (5) years for sludge data] at the treatment facility office in metal file cabinets. Before any result is reported, all raw data and calculations are reviewed for accuracy by someone other than the analyst/lab technician who performed the testing. Depending on the size of the lab/wastewater facility, the individual who performs the review on analytical testing may be another analyst/lab technician, operator or the facility supervisor. In any case, the individual must have sufficient experience to be capable of distinguishing between correct and incorrect data.
It is important that all raw data be kept, no matter how rough in appearance. This information can be very helpful in locating data handling problems. If data contained on any record is transcribed to facilitate summarizing or neatness, the original record must also be kept. Section NR 149.39 (3) specifically requires that records be maintained such that any sample may be traced back to the analyst, date collected, date analyzed, and method used including raw data, intermediate calculations, results, and the final report. In addition, quality control results must be traceable to all of the associated sample results.
A typical wastewater treatment plant operator is charged with a multitude of duties throughout the municipality, and when something has to be overlooked, it tends to be documentation. Unfortunately, documentation is essential to substantiating the quality of your data. A good principle to operate by is that if you did the work - whatever that aspect of the analysis might be-take credit for your efforts, by documenting what you did. The old adage, "If you didn't document it...you didn't do it", also applies.
Finally, s. NR 149.39 (1)(g) requires that all records "shall be handled and stored in a manner that ensures their permanence and security for the required retention period." This section of NR 149 also specifies that "Handwritten records shall be recorded in ink." In keeping with the intent of these requirements, correction fluid of any type, and pens containing "erasable ink" must not be used. If errors are made when making a notation, a single line should be drawn through the entry and the correction entered directly above. Good laboratory practice also requires that corrections made in this manner should be accompanied by the initials of the individual making the correction and the date the correction was made.